문제
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
해설
방향그래프에 맞추어 다익스트라 알고리즘을 이용해 해결한 문제입니다.
다익스트라는 최단경로 탐색 알고리즘으로 음의 간선이 없는 경우에 사용할 수 있는 문제입니다.
DP문제로도 볼 수 있는 이유로 정점에서 다른 정점으로 가는 최단 경로는 다른 최단 경로들로 이루어져 있어 이전의 최단 경로들로 다른 최단경로들을 얻어낼 수 있습니다. 문제에서는 방향 그래프이므로 입력을 양방향이 아닌 단방향으로 구현하여 사용하면 동일하게 해결할 수 있습니다.
작동방식
1. 출발 정점 설정
2. 출발 정점 기준 각 정점의 최소 비용 저장
3. 방문하지 않은 정점 중에서 가장 비용이 적은 정점 선택
4. 해당 정점을 거쳐 특정 정점으로 가는 경우를 고려해 최소비용 갱신
5. 위의 3,4를 반복
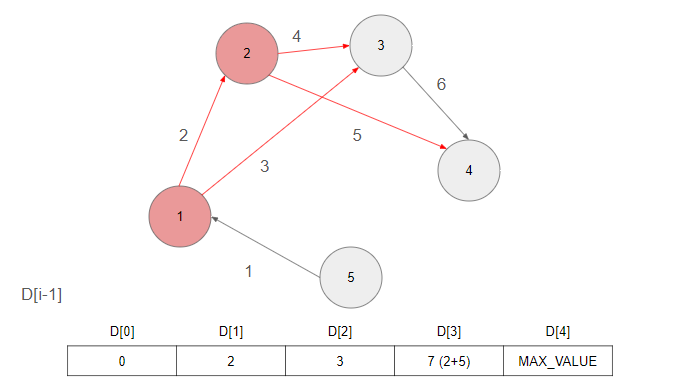
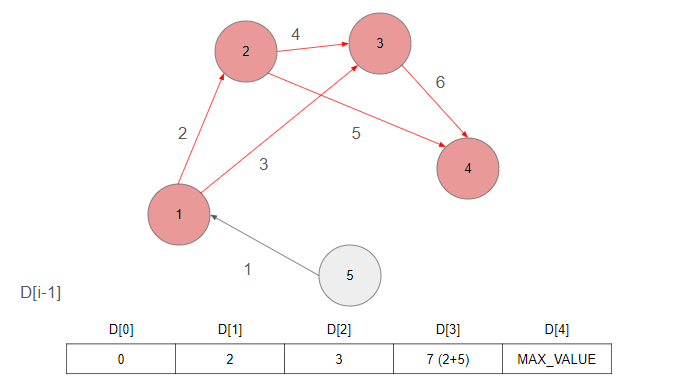
배열 D[i]는 출발 정점부터 i+1점까지의 최단거리입니다.
아래의 그림은 백준의 예시를 기반으로한 그림자료입니다.


코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class Main{
static class Edge{
int v, weight;//정점, 가중치
Edge(int v, int weight){
this.v = v;
this.weight = weight;
}
}
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken()); //정점의 개수 (1부터 V까지 번호 매김) V:5
int E = Integer.parseInt(st.nextToken());// 간선의 개수
int K = Integer.parseInt(br.readLine());//시작정점
List<Edge>[] adj = new ArrayList[V];//V:5 인덱스0~4
for(int i = 0; i < V; i++)
adj[i] = new ArrayList<>();
for(int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
adj[Integer.parseInt(st.nextToken())-1]
.add(new Edge(Integer.parseInt(st.nextToken())-1, Integer.parseInt(st.nextToken())));
}
int[] D = new int[V];
Arrays.fill(D, Integer.MAX_VALUE);
boolean[] check = new boolean[V];
D[K-1] = 0;//dijkstra 시작점이 a정점이라면 D[a] = 0
int min,index;
for(int i = 0; i < V-1; i++) {
min = Integer.MAX_VALUE;//가장 작은 값을 기억할 변수
index = -1; //그 위치를 기억할 변수
for( int j = 0; j < V; j++ ) {
//아직 처리하지 않았으면서, 가장 짧은 거리라면
if(!check[j] && min > D[j]) {
min = D[j];
index = j;
}
}
//연결이 없는 경우 끝
if(index == -1)
break;
//새로운 정점으로부터 갈수있는 경로들을 업데이트
for( Edge next : adj[index] ) {
// check되지 않았으면서, D[next.v]가 D[edge.v] + next.weight 보다 더 크다면 갱신
if( !check[next.v] && D[next.v] > D[index] + next.weight ) {
D[next.v] = D[index] + next.weight;
}
}
//처리된것으로 체크
check[index] = true;
}
for(int i = 0; i < V; i++) {
if( D[i] == Integer.MAX_VALUE)
System.out.println("INF");
else
System.out.println(D[i]);
}
}
}'[IT] 코딩테스트 > [문제 및 풀이] 백준' 카테고리의 다른 글
| [백준] 1987 알파벳 / 자바(Java) (1) | 2023.12.05 |
|---|---|
| [백준] 1600 말이 되고픈 원숭이 / 자바(Java) (2) | 2023.12.04 |
| [백준] 1937 욕심쟁이 판다 / 자바(Java) (1) | 2023.11.30 |
| [백준] 6198 옥상 정원 꾸미기 / 자바(Java) (1) | 2023.11.29 |
| [백준] 4485 녹색 옷 입은 애가 젤다지? / 자바(Java) (1) | 2023.11.28 |



